Logistic Regression in Python - A Step-by-Step Guide

Hey - Nick here! This page is a free excerpt from my new eBook Pragmatic Machine Learning, which teaches you real-world machine learning techniques by guiding you through 9 projects.

Since you're reading my blog, I want to offer you a discount. Click here to buy the book for 70% off now.

In our last article, we learned about the theoretical underpinnings of logistic regression and how it can be used to solve machine learning classification problems.

This tutorial will teach you more about logistic regression machine learning techniques by teaching you how to build logistic regression models in Python.

Table of Contents

You can skip to a specific section of this Python logistic regression tutorial using the table of contents below:

The Data Set We Will Be Using in This Tutorial

The Titanic data set is a very famous data set that contains characteristics about the passengers on the Titanic. It is often used as an introductory data set for logistic regression problems.

In this tutorial, we will be using the Titanic data set combined with a Python logistic regression model to predict whether or not a passenger survived the Titanic crash.

The original Titanic data set is publicly available on Kaggle.com, which is a website that hosts data sets and data science competitions.

To make things easier for you as a student in this course, we will be using a semi-cleaned version of the Titanic data set, which will save you time on data cleaning and manipulation.

The cleaned Titanic data set has actually already been made available for you. You can download the data file by clicking the links below:

Once this file has been downloaded, open a Jupyter Notebook in the same working directory and we can begin building our logistic regression model.

The Imports We Will Be Using in This Tutorial

As before, we will be using multiple open-source software libraries in this tutorial. Here are the imports you will need to run to follow along as I code through our Python logistic regression model:

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

%matplotlib inline

import seaborn as sns

Next, we will need to import the Titanic data set into our Python script.

Importing the Data Set into our Python Script

We will be using pandas' read_csv method to import our csv files into pandas DataFrames called titanic_data.

Here is the code to do this:

titanic_data = pd.read_csv('titanic_train.csv')

Next, let's investigate what data is actually included in the Titanic data set. There are two main methods to do this (using the titanic_data DataFrame specifically):

  • The titanic_data.head(5) method will print the first 5 rows of the DataFrame. You can substitute 5 with whichever number you'd like.
  • You can also print titanic_data.columns, which will show you the column named.

Running the second command (titanic_data.columns) generates the following output:

Index(['PassengerId', 'Survived', 'Pclass', 'Name', 'Sex', 'Age', 'SibSp',

       'Parch', 'Ticket', 'Fare', 'Cabin', 'Embarked'],

      dtype='object'

These are the names of the columns in the DataFrame. Here are brief explanations of each data point:

  • PassengerId: a numerical identifier for every passenger on the Titanic.
  • Survived: a binary identifier that indicates whether or not the passenger survived the Titanic crash. This variable will hold a value of 1 if they survived and 0 if they did not.
  • Pclass: the passenger class of the passenger in question. This can hold a value of 1, 2, or 3, depending on where the passenger was located in the ship.
  • Name: the passenger's name.`
  • Sex: male or female.
  • Age: the age (in years) of the passenger.
  • SibSp: the number of siblings and spouses aboard the ship.
  • Parch: the number of parents and children aboard the ship.
  • Ticket: the passenger's ticket number.
  • Fare: how much the passenger paid for their ticket on the Titanic.
  • Cabin: the passenger's cabin number.
  • Embarked: the port where the passenger embarked (C = Cherbourg, Q = Queenstown, S = Southampton)

Next up, we will learn more about our data set by using some basic exploratory data analysis techniques.

Learning About Our Data Set With Exploratory Data Analysis

The Prevalence of Each Classification Category

When using machine learning techniques to model classification problems, it is always a good idea to have a sense of the ratio between categories. For this specific problem, it's useful to see how many survivors vs. non-survivors exist in our training data.

An easy way to visualize this is using the seaborn plot countplot. In this example, you could create the appropriate seasborn plot with the following Python code:

sns.countplot(x='Survived', data=titanic_data)

This generates the following plot:

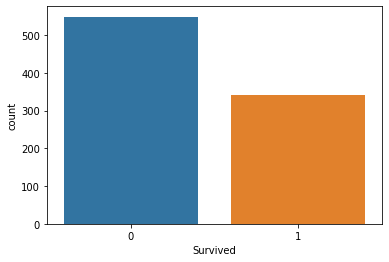
A seaborn countplot

As you can see, we have many more incidences of non-survivors than we do of survivors.

Survival Rates Between Genders

It is also useful to compare survival rates relative to some other data feature. For example, we can compare survival rates between the Male and Female values for Sex using the following Python code:

sns.countplot(x='Survived', hue='Sex', data=titanic_data)

This generates the following plot:

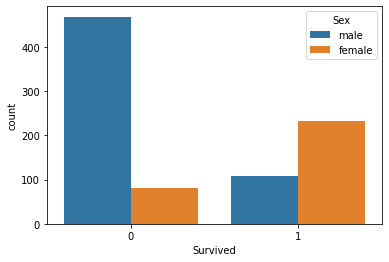
A seaborn countplot with a Sex hue

As you can see, passengers with a Sex of Male were much more likely to be non-survivors than passengers with a Sex of Female.

Survival Rates Between Passenger Classes

We can perform a similar analysis using the Pclass variable to see which passenger class was the most (and least) likely to have passengers that were survivors.

Here is the code to do this:

sns.countplot(x='Survived', hue='Pclass', data=titanic_data)

This generates the following plot:

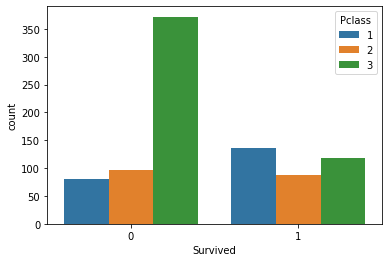
A seaborn countplot with a Pclass hue

The most noticeable observation from this plot is that passengers with a Pclass value of 3 - which indicates the third class, which was the cheapest and least luxurious - were much more likely to die when the Titanic crashed.

The Age Distribution of Titanic Passengers

One other useful analysis we could perform is investigating the age distribution of Titanic passengers. A histogram is an excellent tool for this.

You can generate a histogram of the Age variable with the following code:

plt.hist(titanic_data['Age'].dropna())

Note that the dropna() method is necessary since the data set contains several nulls values.

Here is the histogram that this code generates:

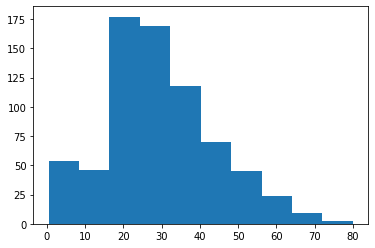
A histogram of age variables from the titanic data set

As you can see, there is a concentration of Titanic passengers with an Age value between 20 and 40.

The Ticket Price Distribution of Titanic Passengers

The last exploratory data analysis technique that we will use is investigating the distribution of fare prices within the Titanic data set.

You can do this with the following code:

plt.hist(titanic_data['Fare'])

This generates the following plot:

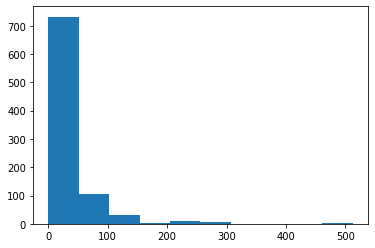
A histogram of fare variables from the titanic data set

As you can see, there are three distinct groups of Fare prices within the Titanic data set. This makes sense because there are also three unique values for the Pclass variable. The difference Fare groups correspond to the different Pclass categories.

Since the Titanic data set is a real-world data set, it contains some missing data. We will learn how to deal with missing data in the next section.

Removing Null Data From Our Data Set

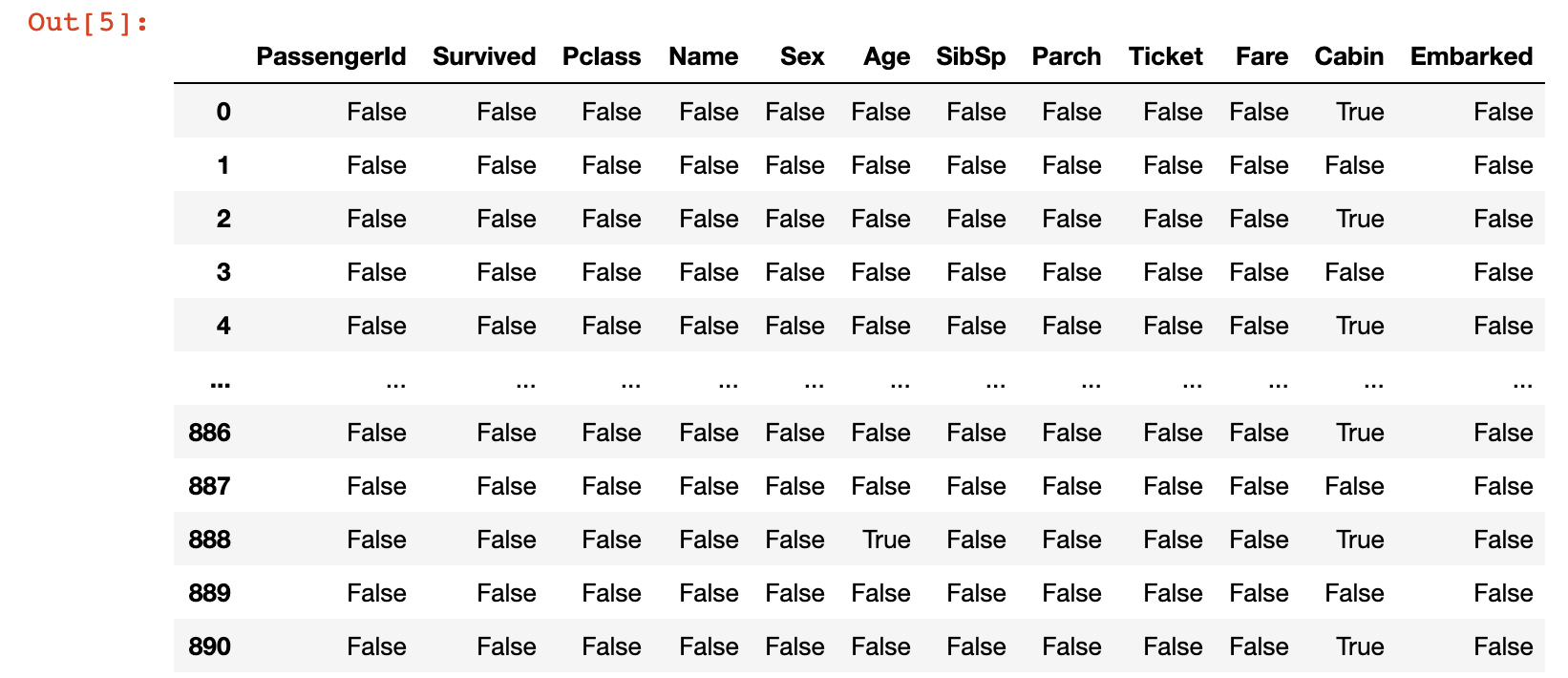
To start, let's examine where our data set contains missing data. To do this, run the following command:

titanic_data.isnull()

This will generate a DataFrame of boolean values where the cell contains True if it is a null value and False otherwise. Here is an image of what this looks like:

A DataFrame of boolean values indicating where null data exists

A far more useful method for assessing missing data in this data set is by creating a quick visualization. To do this, we can use the seaborn visualization library. Here is quick command that you can use to create a heatmap using the seaborn library:

sns.heatmap(titanic_data.isnull(), cbar=False)

Here is the visualization that this generates:

A DataFrame of boolean values indicating where null data exists

In this visualization, the white lines indicate missing values in the dataset. You can see that the Age and Cabin columns contain the majority of the missing data in the Titanic data set.

The Age column in particular contains a small enough amount of missing that that we can fill in the missing data using some form of mathematics. On the other hand, the Cabin data is missing enough data that we could probably remove it from our model entirely.

The process of filling in missing data with average data from the rest of the data set is called imputation. We will now use imputation to fill in the missing data from the Age column.

The most basic form of imputation would be to fill in the missing Age data with the average Age value across the entire data set. However, there are better methods.

We will fill in the missing Age values with the average Age value for the specific Pclass passenger class that the passenger belongs to. To understand why this is useful, consider the following boxplot:

sns.boxplot(titanic_data['Pclass'], titanic_data['Age'])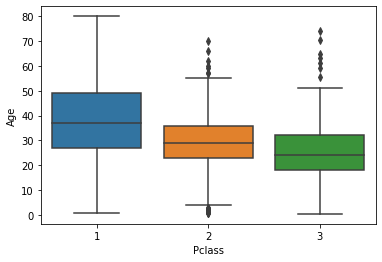

A boxplot of age values stratified by passenger classes

As you can see, the passengers with a Pclass value of 1 (the most expensive passenger class) tend to be the oldest while the passengers with a Pclass value of 3 (the cheapest) tend to be the youngest. This is very logical, so we will use the average Age value within different Pclass data to imputate the missing data in our Age column.

The easiest way to perform imputation on a data set like the Titanic data set is by building a custom function. To start, we will need to determine the mean Age value for each Pclass value.

#Pclass value 1

titanic_data[titanic_data['Pclass'] == 1]['Age'].mean()

#Pclass value 2

titanic_data[titanic_data['Pclass'] == 2]['Age'].mean()

#Pclass 3

titanic_data[titanic_data['Pclass'] == 2]['Age'].mean()

Here is the final function that we will use to imputate our missing Age variables:

def impute_missing_age(columns):

    age = columns[0]

    passenger_class = columns[1]

    

    if pd.isnull(age):

        if(passenger_class == 1):

            return titanic_data[titanic_data['Pclass'] == 1]['Age'].mean()

        elif(passenger_class == 2):

            return titanic_data[titanic_data['Pclass'] == 2]['Age'].mean()

        elif(passenger_class == 3):

            return titanic_data[titanic_data['Pclass'] == 3]['Age'].mean()

        

    else:

        return age

Now that this imputation function is complete, we need to apply it to every row in the titanic_data DataFrame. Python's apply method is an excellent tool for this:

titanic_data['Age'] = titanic_data[['Age', 'Pclass']].apply(impute_missing_age, axis = 1)

Now that we have performed imputation on every row to deal with our missing Age data, let's investigate our original boxplot:

sns.heatmap(titanic_data.isnull(), cbar=False)

You wil notice there is no longer any missing data in the Age column of our pandas DataFrame!

You might be wondering why we spent so much time dealing with missing data in the Age column specifically. It is because given the impact of Age on survival for most disasters and diseases, it is a variable that is likely to have high predictive value within our data set.

Now that we have an understanding of the structure of this data set and have removed its missing data, let's begin building our logistic regression machine learning model.

Building a Logistic Regression Model

It is now time to remove our logistic regression model.

Removing Columns With Too Much Missing Data

First, let's remove the Cabin column. As we mentioned, the high prevalence of missing data in this column means that it is unwise to impute the missing data, so we will remove it entirely with the following code:

titanic_data.drop('Cabin', axis=1, inplace = True)

Next, let's remove any additional columns that contain missing data with the pandas dropna() method:

titanic_data.dropna(inplace = True)

Handling Categorical Data With Dummy Variables

The next task we need to handle is dealing with categorical features. Namely, we need to find a way to numerically work with observations that are not naturally numerical.

A great example of this is the Sex column, which has two values: Male and Female. Similarly, the Embarked column contains a single letter which indicates which city the passenger departed from.

To solve this problem, we will create dummy variables. These assign a numerical value to each category of a non-numerical feature.

Fortunately, pandas has a built-in method called get_dummies() that makes it easy to create dummy variables. The get_dummies method does have one issue - it will create a new column for each value in the DataFrame column.

Let's consider an example to help understand this better. If we call the get_dummies() method on the Age column, we get the following output:

pd.get_dummies(titanic_data['Sex'])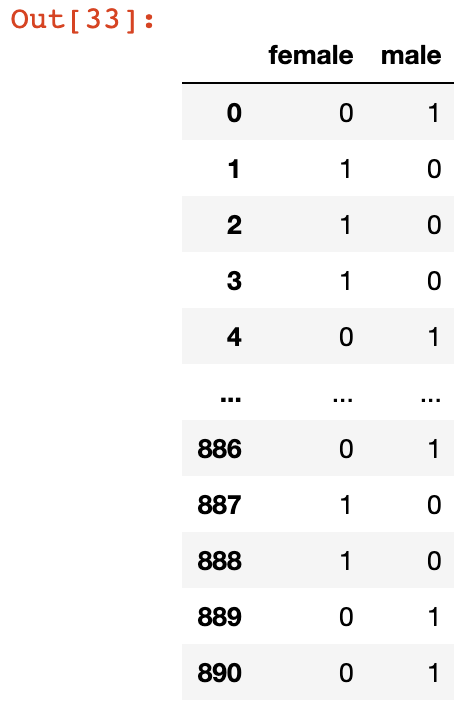

An example of the pandas get_dummies method

As you can see, this creates two new columns: female and male. These columns will both be perfect predictors of each other, since a value of 0 in the female column indicates a value of 1 in the male column, and vice versa.

This is called multicollinearity and it significantly reduces the predictive power of your algorithm. To remove this, we can add the argument drop_first = True to the get_dummies method like this:

pd.get_dummies(titanic_data['Sex'], drop_first = True)

Now, let's create dummy variable columns for our Sex and Embarked columns, and assign them to variables called sex and embarked.

sex_data = pd.get_dummies(titanic_data['Sex'], drop_first = True)

embarked_data = pd.get_dummies(titanic_data['Embarked'], drop_first = True)

There is one important thing to note about the embarked variable defined below. It has two columns: Q and S, but since we've already removed one other column (the C column), neither of the remaining two columns are perfect predictors of each other, so multicollinearity does not exist in the new, modified data set.

Adding Dummy Variables to the pandas DataFrame

Next we need to add our sex and embarked columns to the DataFrame.

You can concatenate these data columns into the existing pandas DataFrame with the following code:

titanic_data = pd.concat([titanic_data, sex_data, embarked_data], axis = 1)

Now if you run the command print(titanic_data.columns), your Jupyter Notebook will generate the following output:

Index(['PassengerId', 'Survived', 'Pclass', 'Name', 'Sex', 'Age', 'SibSp',

       'Parch', 'Ticket', 'Fare', 'Embarked', 'male', 'Q', 'S'],

      dtype='object')

The existence of the male, Q, and S columns shows that our data was concatenated successfully.

Removing Unnecessary Columns From The Data Set

This means that we can now drop the original Sex and Embarked columns from the DataFrame. There are also other columns (like Name , PassengerId, Ticket) that are not predictive of Titanic crash survival rates, so we will remove those as well. The following code handles this for us:

titanic_data.drop(['Name', 'Ticket', 'Sex', 'Embarked'], axis = 1, inplace = True)

If you print titanic_data.columns now, your Jupyter Notebook will generate the following output:

Index(['Survived', 'Pclass', 'Age', 'SibSp', 'Parch', 'Fare',

       'male', 'Q', 'S'],

      dtype='object'

The DataFrame now has the following appearance:

The final DataFrame for our logistic regression model

As you can see, every field in this data set is now numeric, which makes it an excellent candidate for a logistic regression machine learning algorithm.

Creating Training Data and Test Data

Next, it's time to split our titatnic_data into training data and test data. As before, we will use built-in functionality from scikit-learn to do this.

First, we need to divide our data into x values (the data we will be using to make predictions) and y values (the data we are attempting to predict). The following code handles this:

y_data = titanic_data['Survived']

x_data = titanic_data.drop('Survived', axis = 1)

Next, we need to import the train_test_split function from scikit-learn. The following code executes this import:

from sklearn.model_selection import train_test_split

Lastly, we can use the train_test_split function combined with list unpacking to generate our training data and test data:

x_training_data, x_test_data, y_training_data, y_test_data = train_test_split(x_data, y_data, test_size = 0.3)

Note that in this case, the test data is 30% of the original data set as specified with the parameter test_size = 0.3.

We have now created our training data and test data for our logistic regression model. We will train our model in the next section of this tutorial.

Training the Logistic Regression Model

To train our model, we will first need to import the appropriate model from scikit-learn with the following command:

from sklearn.linear_model import LogisticRegression

Next, we need to create our model by instantiating an instance of the LogisticRegression object:

model = LogisticRegression()

To train the model, we need to call the fit method on the LogisticRegression object we just created and pass in our x_training_data and y_training_data variables, like this:

model.fit(x_training_data, y_training_data)

Our model has now been trained. We will begin making predictions using this model in the next section of this tutorial.

Making Predictions With Our Logistic Regression Model

Let's make a set of predictions on our test data using the model logistic regression model we just created. We will store these predictions in a variable called predictions:

predictions = model.predict(x_test_data)

Our predictions have been made. Let's examine the accuracy of our model next.

Measuring the Performance of a Logistic Regression Machine Learning Model

scikit-learn has an excellent built-in module called classification_report that makes it easy to measure the performance of a classification machine learning model. We will use this module to measure the performance of the model that we just created.

First, let's import the module:

from sklearn.metrics import classification_report

Next, let's use the module to calculate the performance metrics for our logistic regression machine learning module:

classification_report(y_test_data, predictions)

Here is the output of this command:

             precision    recall  f1-score   support

           0       0.83      0.87      0.85       169

           1       0.75      0.68      0.72        98

    accuracy                           0.80       267

   macro avg       0.79      0.78      0.78       267

weighted avg       0.80      0.80      0.80       267

If you're interested in seeing the raw confusion matrix and calculating the performance metrics manually, you can do this with the following code:

from sklearn.metrics import confusion_matrix

print(confusion_matrix(y_test_data, predictions))

This generates the following output:

[[145  22]

 [ 30  70]]

The Full Code for This Tutorial

You can view the full code for this tutorial in this GitHub repository. It is also pasted below for your reference:

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

%matplotlib inline

import seaborn as sns

#Import the data set

titanic_data = pd.read_csv('titanic_train.csv')

#Exploratory data analysis

sns.heatmap(titanic_data.isnull(), cbar=False)

sns.countplot(x='Survived', data=titanic_data)

sns.countplot(x='Survived', hue='Sex', data=titanic_data)

sns.countplot(x='Survived', hue='Pclass', data=titanic_data)

plt.hist(titanic_data['Age'].dropna())

plt.hist(titanic_data['Fare'])

sns.boxplot(titanic_data['Pclass'], titanic_data['Age'])

#Imputation function

def impute_missing_age(columns):

    age = columns[0]

    passenger_class = columns[1]

    

    if pd.isnull(age):

        if(passenger_class == 1):

            return titanic_data[titanic_data['Pclass'] == 1]['Age'].mean()

        elif(passenger_class == 2):

            return titanic_data[titanic_data['Pclass'] == 2]['Age'].mean()

        elif(passenger_class == 3):

            return titanic_data[titanic_data['Pclass'] == 3]['Age'].mean()

        

    else:

        return age

#Impute the missing Age data

titanic_data['Age'] = titanic_data[['Age', 'Pclass']].apply(impute_missing_age, axis = 1)

#Reinvestigate missing data

sns.heatmap(titanic_data.isnull(), cbar=False)

#Drop null data

titanic_data.drop('Cabin', axis=1, inplace = True)

titanic_data.dropna(inplace = True)

#Create dummy variables for Sex and Embarked columns

sex_data = pd.get_dummies(titanic_data['Sex'], drop_first = True)

embarked_data = pd.get_dummies(titanic_data['Embarked'], drop_first = True)

#Add dummy variables to the DataFrame and drop non-numeric data

titanic_data = pd.concat([titanic_data, sex_data, embarked_data], axis = 1)

titanic_data.drop(['Name', 'PassengerId', 'Ticket', 'Sex', 'Embarked'], axis = 1, inplace = True)

#Print the finalized data set

titanic_data.head()

#Split the data set into x and y data

y_data = titanic_data['Survived']

x_data = titanic_data.drop('Survived', axis = 1)

#Split the data set into training data and test data

from sklearn.model_selection import train_test_split

x_training_data, x_test_data, y_training_data, y_test_data = train_test_split(x_data, y_data, test_size = 0.3)

#Create the model

from sklearn.linear_model import LogisticRegression

model = LogisticRegression()

#Train the model and create predictions

model.fit(x_training_data, y_training_data)

predictions = model.predict(x_test_data)

#Calculate performance metrics

from sklearn.metrics import classification_report

print(classification_report(y_test_data, predictions))

#Generate a confusion matrix

from sklearn.metrics import confusion_matrix

print(confusion_matrix(y_test_data, predictions))

Final Thoughts

In this tutorial, you learned how to build logistic regression machine learning models in Python.

Here is a brief summary of what you learned in this article:

  • Why the Titanic data set is often used for learning machine learning classification techniques
  • How to perform exploratory data analysis when working with a data set for classification machine learning problems
  • How to handle missing data in a pandas DataFrame
  • What imputation means and how you can use it to fill in missing data
  • How to create dummy variables for categorical data in machine learning data sets
  • How to train a logistic regression machine learning model in Python
  • How to make predictions using a logistic regression model in Python
  • How to the scikit-learn's classification_report to quickly calculate performance metrics for machine learning classification problems