The vanishing gradient problem has historically been one of the largest barriers to the success of recurrent neural networks.
Because of this, having an understanding of the vanishing gradient problem is important before you build your first RNN.
This article will explain the vanishing gradient problem in plain English, including a discussion of the most useful solutions to this interesting problem.
Table of Contents
You can skip to a specific section of this recurrent neural network tutorial using the table of contents below:
What Is The Vanishing Gradient Problem?
Before we dig in to the details of the vanishing gradient problem, it's helpful to have some understanding of how the problem was initially discovered.
The vanishing gradient problem was discovered by Sepp Hochreiter, a German computer scientist who has had an influential role in the development of recurrent neural networks in deep learning.
Now let's explore the vanishing gradient problem in detail. As its name implies, the vanishing gradient problem is related to deep learning gradient descent algorithms. Recall that a gradient descent algorithm looks something like this:
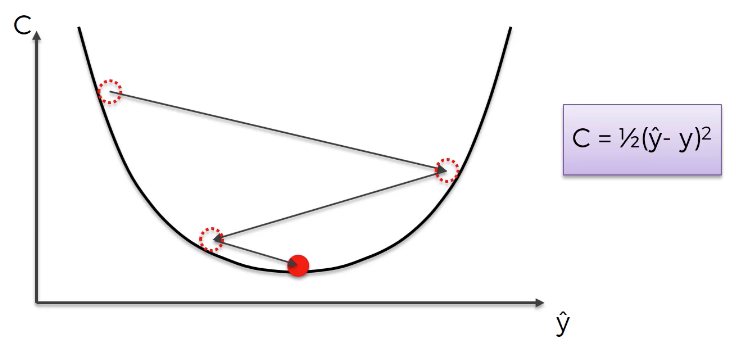
This gradient descent algorithm is then combined with a backpropagation algorithm to update the synapse weights throughout the neural network.
Recurrent neural networks behave slightly differently because the hidden layer of one observation is used to train the hidden layer of the next observation. This means that
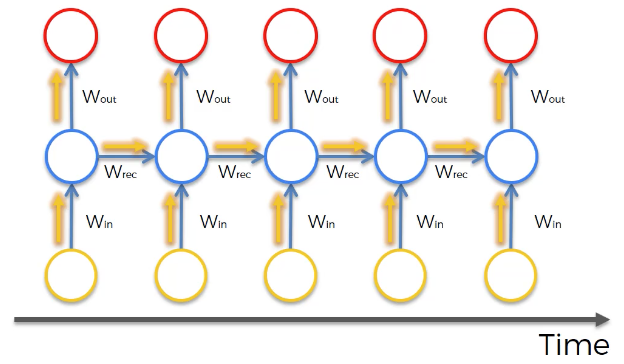
The cost function of the neural net is calculated for each observation in the data set. These cost function values are depicted at the top of the following image:
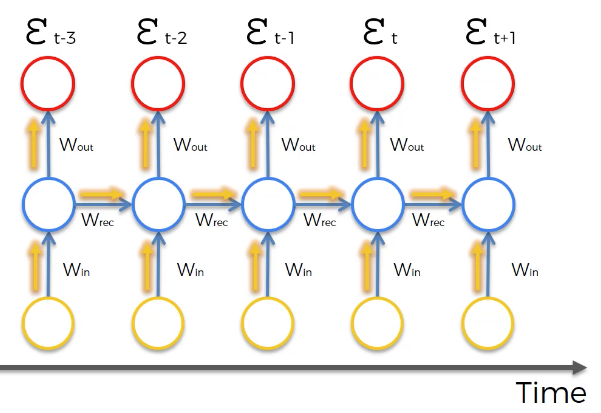
The vanishing gradient problem occurs when the backpropagation algorithm moves back through all of the neurons of the neural net to update their weights. The nature of recurrent neural networks means that the cost function computed at a deep layer of the neural net will be used to change the weights of neurons at shallower layers.
The mathematics that computes this change is multiplicative, which means that the gradient calculated in a step that is deep in the neural network will be multiplied back through the weights earlier in the network. Said differently, the gradient calculated deep in the network is "diluted" as it moves back through the net, which can cause the gradient to vanish - giving the name to the vanishing gradient problem!
The actual factor that is multiplied through a recurrent neural network in the backpropagation algorithm is referred to by the mathematical variable Wrec. It poses two problems:
- When
Wrecis small, you experience a vanishing gradient problem - When
Wrecis large, you experience an exploding gradient problem
Note that both of these problems are generally referred to by the simpler name of the "vanishing gradient problem".
To summarize, the vanishing gradient problem is caused by the multiplicative nature of the backpropagation algorithm. It means that gradients calculated at a deep stage of the recurrent neural network either have too small of an impact (in a vanishing gradient problem) or too large of an impact (in an exploding gradient problem) on the weights of neurons that are shallower in the neural net.
How to Solve The Vanishing Gradient Problem
There are a number of strategies that can be used to solve the vanishing gradient problem. We will explore strategies for both the vanishing gradient and exploding gradient problems separately. Let's start with the latter.
Solving the Exploding Gradient Problem
For exploding gradients, it is possible to use a modified versino of the backpropagation algorithm called truncated backpropagation. The truncated backpropagation algorithm limits that number of timesteps that the backproporation will be performed on, stopping the algorithm before the exploding gradient problem occurs.
You can also introduce penalties, which are hard-coded techniques for reduces a backpropagation's impact as it moves through shallower layers in a neural network.
Lastly, you could introduce gradient clipping, which introduces an artificial ceiling that limits how large the gradient can become in a backpropagation algorithm.
Solving the Vanishing Gradient Problem
Weight initialization is one technique that can be used to solve the vanishing gradient problem. It involves artificially creating an initial value for weights in a neural network to prevent the backpropagation algorithm from assigning weights that are unrealistically small.
You could also use echo state networks, which is a specific type of neural network designed to avoid the vanishing gradient problem. Echo state networks are outside the scope of this course. Having knowledge of their existence is sufficient for now.
The most important solution to the vanishing gradient problem is a specific type of neural network called Long Short-Term Memory Networks (LSTMs), which were pioneered by Sepp Hochreiter and Jürgen Schmidhuber. Recall that Mr. Hochreiter was the scientist who originally discovered the vanishing gradient problem.
LSTMs are used in problems primarily related to speech recognition, with one of the most notable examples being Google using an LSTM for speech recognition in 2015 and experiencing a 49% decrease in transcription errors.
LSTMs are considered to be the go-to neural net for scientists interested in implementing recurrent neural networks. We will be largely focusing on LSTMs through the remainder of this course.
Final Thoughts
In this article, you learned about the vanishing gradient problem of recurrent neural networks.
Here is a brief summary of what we discussed:
- That Sepp Hochreiter was the first scientist to discover the vanishing gradient problem in recurrent neural networks
- What the vanishing gradient problem (and its cousin, the exploding gradient problem) involves
- The role of
Wrecin vanishing gradient problems and exploding gradient problems - How vanishing gradient problems and exploding gradient problems are solved
- The role of LSTMs as the most common solution to the vanishing gradient problem
