How to Write a Merge Sort Algorithm in Java
Java is an object-oriented programming language that allows cross-platform integration. Java is highly versatile and known for its fast performance, security, and high reliability.
It is always rewarding to know how to implement sorting algorithms, and Java is no exception. Java is an object-oriented programming language, so it allows you to write sorting algorithms as classes and implement them easily using sorter objects.
In this tutorial, you will learn how to apply a specific sorting algorithm in Java. Specifically, this article will show you how to write a merge sort algorithm in Java.
Why is Sorting Important?
Let’s consider why sorting can be so important to us.
Imagine your computer has tons of data about all the phone numbers in the world. Let’s say whenever you want someone’s phone number, you only have to enter their name. However, as there are billions of phone numbers, it will take lots of time to find the number you want. Just like it will take lots of time to find the card you want from a deck of shuffled cards.
Sorting makes it easier to find an item from a big list quite efficiently and faster.
How does Merge Sort work?
Merge sort is an algorithm that sorts lists and arrays based on the Divide and Conquer technique. It repeatedly divides the list or array into halves until each segment has a single value. We call it a recursive algorithm for this reason. Merge sort supports arrays with both odd and even lengths.
Once all segments contain a single value, they are considered sorted. The algorithm then begins to merge adjacent segments after sorting them. By the time all segments are sorted and merged, the entire list will be sorted. Don’t worry if you’re confused, the example below will clear things for you.
Let’s consider the array [40, 29, 45, 5, 11, 84, 12], which has 7 numbers.
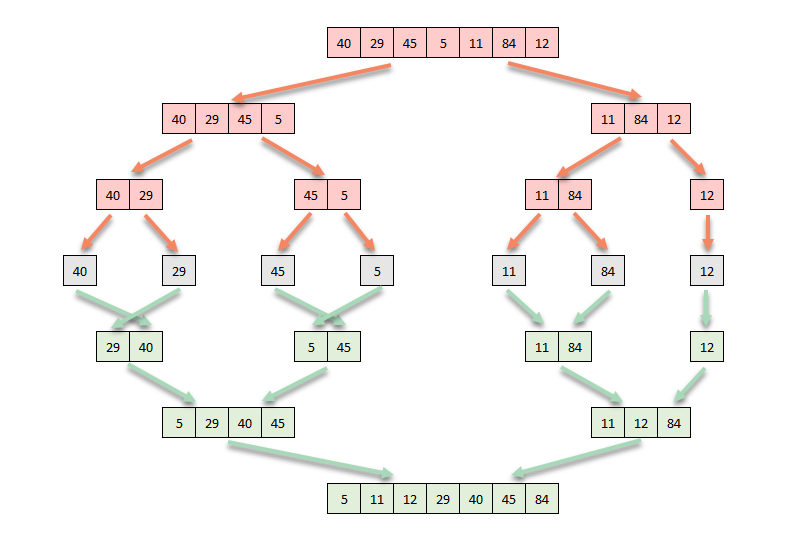
The transition from the topmost level of the following diagram to the second level shows how the array is divided in half. As this array’s length is odd, the array is divided 4:3. However, had it been an even number, it would have been divided into two equal parts.
We can call the two halves at the second level, the left-sub-array and right-sub-array. As displayed in the diagram, all segments are divided recursively until they each have a single number. Now each segment is considered sorted (the fourth level - marked in Grey).
Now the algorithm begins the merge sort process. It merges adjacent segments [4,29], [45,5], [11,4], [12] while sorting each of them. The result is displayed on the fifth level. Merging continues recursively until all segments are sorted and merged into a single array (last level).
Implementation in Java
Let’s consider how this algorithm can be implemented in Java.
We start by creating a MergeSort class with a mergeArray() method and a sortArray() method. The sortArray method is a recursive one, which means it invokes itself inside its own code. Before we try to understand the whole class, let’s consider the methods one by one.
The mergeArray() method
void mergeArray(int sortableArray[], int startPoint, int midPoint, int endPoint) {
// Code to be added here
}This method accepts an unsorted array along with its start-point, mid-point, and end-point. It’s important that you understand the fact that the unsorted array could also be a sub-array divided from a super-array in the preceding level.
We need to divide the unsorted array (sortableArray) into two parts, as shown below, producing two sub-arrays - LeftArray and RightArray.
int left = midPoint - startPoint + 1;
int right = endPoint - midPoint;
int LeftArray[] = new int[left];
int RightArray[] = new int[right];
for (int x = 0; x < left; ++x) {
LeftArray[x] = sortableArray[startPoint + x];
}
for (int x = 0; x < right; ++x) {
RightArray[x] = sortableArray[midPoint + 1 + x];
}Then we can compare LeftArray and RightArray at each level and combine them to produce a sorted sub-array and overwrite it on the input array as follows.
int x = 0;
int y = 0;
int z = startPoint;
while (x < left && y < right) {
if (LeftArray[x] <= RightArray[y]) {
sortableArray[z] = LeftArray[x];
x++;
} else {
sortableArray[z] = RightArray[y];
y++;
}
z++;
}
while (x < left) {
sortableArray[z] = LeftArray[x];
x++;
z++;
}
while (y < right) {
sortableArray[z] = RightArray[y];
y++;
z++;
}To summarize, the functionality of mergeArray() is to take an array in, sort its values, and overwrite it prior to returning it.
That’s it for the mergeArray() method.
The sortArray() method
void sortArray(int arr[], int startingPoint, int endingPoint) {
// Code to be added here
}The sortArray() method takes in an unsorted array along with its start-point and end-point. Merge sorts recursively divide an array until it contains a single value. The sortArray() method below takes in an array or a subarray and divides it into two parts and resends them to the sortArray() method, so that the process continues recursively.
if (startingPoint < endingPoint) {
int middlePoint = (startingPoint + endingPoint) / 2;
sortArray(arr, startingPoint, middlePoint);
sortArray(arr, middlePoint + 1, endingPoint);
mergeArray(arr, startingPoint, middlePoint, endingPoint);
}To bring more clarity, let’s consider an array of 7 numbers.

- If this array is fed into our program, the sortArray() method will pass its first and second halves separately into the sortArray() method. The sortArray() will recursively divide it into sub-arrays until each segment has only a single value.
- Then the first sortArray() method inside the main instance of sortArray() will take the first half of the main array.

- It will continue to divide the array until it is down to a single element.

- At this point, considering the ‘if statement’ that checks startingPoint < endingPoint, the sortArray() recursion will come to an end and will move to the mergeArray() method allowing it to merge two number elements.
- Going out of the recursion, it will keep merging sub-arrays, and finally output the completely sorted original array.
The Complete Code
Here is the full code of the Merge Sort program. Simply define unsortedArray with any array you like and watch the merge sort algorithm do its magic.
class MergeSort {
void mergeArray(int sortableArray[], int startPoint, int midPoint, int endPoint) {
int left = midPoint - startPoint + 1;
int right = endPoint - midPoint;
int LeftArray[] = new int[left];
int RightArray[] = new int[right];
for (int x = 0; x < left; ++x) {
LeftArray[x] = sortableArray[startPoint + x];
}
for (int x = 0; x < right; ++x) {
RightArray[x] = sortableArray[midPoint + 1 + x];
}
int x = 0;
int y = 0;
int z = startPoint;
while (x < left && y < right) {
if (LeftArray[x] <= RightArray[y]) {
sortableArray[z] = LeftArray[x];
x++;
} else {
sortableArray[z] = RightArray[y];
y++;
}
z++;
}
while (x < left) {
sortableArray[z] = LeftArray[x];
x++;
z++;
}
while (y < right) {
sortableArray[z] = RightArray[y];
y++;
z++;
}
}
void sortArray(int arr[], int startingPoint, int endingPoint) {
if (startingPoint < endingPoint) {
int middlePoint = (startingPoint + endingPoint) / 2;
sortArray(arr, startingPoint, middlePoint);
sortArray(arr, middlePoint + 1, endingPoint);
mergeArray(arr, startingPoint, middlePoint, endingPoint);
}
}
}
class MergeSortExample{
public static void main(String args[])
{
int unsortedArray[] = {40, 29, 45, 5, 11, 84, 12};
MergeSort mergeSort = new MergeSort();
mergeSort.sortArray(unsortedArray, 0, unsortedArray.length-1);
System.out.println();
for(int item: unsortedArray)
{
System.out.print(item+" ");
}
System.out.println();
}
}Time and Space Complexities
Time and space complexities can be thought of as two main performance indicators of how algorithms work. In simple terms, time and space complexities define how much resources an algorithm requires while performing its intended task. Both of these indicators are considered under best, average, and worst cases for a more holistic understanding of each algorithm.
At present, the time–memory trade-off has become more lenient towards memory due to advancements in memory technologies. Therefore when writing algorithms, generally space complexity is not considered that significantly compared to time complexity.
It should also be noted that time complexity does not necessarily mean how much time an algorithm requires to complete its task. In a more practical sense, it gives an idea about the order of steps it requires to solve a problem.
The time complexity is indicated by O(nlogn) in Mert Sort algorithms. Let’s look at the following steps of the Merge Sort algorithm to clarify this point further:
- At each level, before an array is divided in half, the midpoint is always calculated, and it has a time complexity of O(1).
- Once the array is separated into numbers, each right and left portions of n/2 are sorted recursively, giving O(logn)
- At each incremental level, the merging of n elements takes O(n) time.
As O(n) is higher than O(1), we can neglect O(1). It leaves us with a time complexity value of O(nlogn) for merge sort for the best, average, and worst cases.
The following table summarizes complexities for Merge Sort:
| Time Complexity | Space Complexity | ||
| Best | Average | Worst | Worst |
| O(nlogn) | O(nlogn) | O(nlogn) | O(n) |
Conclusion
As much as Java is favoured as a programming language among developers, Merge Sort is very much favoured due to its time complexity. Although this is not a must-know, being aware of it can save you a lot of time, literally.
If you are ever implementing Merge Sort, there are a few things to keep in mind:
- Merge sort is a divide-and-conquer algorithm. It recursively calls itself until arrays are broken down to their number elements. Then it builds the array back while sorting them at each step.
- Merge sort has a time complexity of O(nlogn), which represents one of the fastest sorting algorithms. However, there is always the trade-off of having to require a bit of additional space to store the elements.
- Merge sort is best suited for sorting Linked Lists.
I hope you enjoyed this tutorial.
Have a good day!
