How to Write an Insertion Sort Algorithm in Java
Computer programmers should be familiar with a number of different sorting algorithms.
In this article I'll explain how you can write an insertion sort algorithm in Java. I'll spend the first half of the article explaining how the insertion sort algorithm works. You'll learn how to code an insertion sort algorithm near the end of this tutorial.
Table of Contents
You can skip to a specific section of this Java insertion sort algorithm using the table of contents below:
What is an Insertion Sort Algorithm?
Insertion sort is a straightforward sorting algorithm suited to small data sets. With every iteration, the removes takes an element from the array, compares it against the largest number within the array, and moves the component to its correct location.
Below here is the list of items, let us sort them in increasing order. In this example, the items will simply be integers. Let us look at this sample list of items:
| 5 | 8 | 1 | 3 | 9 | 6 |
|---|
We have a list of six items that we want to sort and we'll number them from zero to five (0=>5). Then the sample will be like this:
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 5 | 8 | 1 | 3 | 9 | 6 |
The first item is 5 which is already sorted because insertion sort is sourced from the left, so the definition sorted to the left means that all items to the left of an item are smaller than all items to the right.
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 5 | 8 | 1 | 3 | 9 | 6 |
So you can see that:
- Item 0 is equal to 5
- Item 1 is equal to 8.
- Item 2 is equal to 1
- Item 3 is equal to 3
- Item 4 is equal to 9
- Item 5 is equal to 6
The insertion sort starts from the first K (all the values in the array which K = 5, K = 8, K = 1, K = 3, K = 9, K = 6) value from the left which is the first comparison. When K = 5, which is the first iteration from the left has no value to be compared to, therefore 5 is already an assorted sorted (all items from the left are smaller) situation. Every first value from the left is assorted.
Meaning we will start our insertion sort at the item number which is 8, so we will set our key value K equals 8 (K = 8).
Now our second comparison is to the item 1 which is 8, so the item 8 (K = 8) is going to check if the item is less than 5, well it is not, then 8 is going to sit where it was, and going to be considered assorted.
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 5 | 8 | 1 | 3 | 9 | 6 |
Next we will look at item number 2, and in our list which is 1 (K =1). So we will assign K = 1 by comparing K if it is less than 8 if it yes. If yes, it is less than 8, so 8 is going to swap with 1. Our K value has not yet changed, K is going to be compared to 5 too, and if K is less than 5, then the 5 is going to swap with 1. Thus, item 2 is now sorted.
Here is how our array has been rearrange:
Before swapping:
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 5 | 8 | 1 | 3 | 9 | 6 |
After swapping:
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 5 | 8 | 3 | 9 | 6 |
So we are going to jump to our next step which is item number 3, and in the list, item 3 is equal to 3 (K = 3). We are going to compare 3 to 8 (K < 3), if it yes, then 8 is going to swap with 1, and comparing K to 5 (K < 3), It is yes, then the item 5 is going to swap to 1, and finally comparing to 1(K < 3). Then the arrangement will be like this:
Before swapping:
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 5 | 8 | 1 | 3 | 9 | 6 |
After swapping:
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 3 | 5 | 8 | 9 | 6 |
So we are going to jump to our next step which is item number 4, and in the list, item 4 is equal to 9 (K = 9). We are going to compare 3 to 8 (K < 8), if it yes, then 8 is going to swap with 9, but it is not, then 9 is going to remain at its place.
Before swapping:
| 5 | 8 | 1 | 3 | 9 | 6 |
After swapping:
| 1 | 3 | 5 | 8 | 9 | 6 |
So we are finally going to jump to the next step which is item number 5, and in the list, item 5 is equal to 6 (K = 6). We are going to compare 6 to 9 (K < 9), if it yes, then 9 is going to swap with 6, and comparing K to 8 (K < 8), It is yes, then the item 8 is going to swap to 6, and finally comparing to 1(K < 5). Then the arrangement will be like this:
Before:
| 5 | 8 | 1 | 3 | 9 | 6 |
After swapping:
| 1 | 3 | 5 | 6 | 8 | 9 |
So the sort is now finished. Here is our sorted array:
| 1 | 3 | 5 | 6 | 8 | 9 |
The insertion sort is not a fast sorting algorithm because it uses nested loops to shift items into place. It is useful only for small data sets.
Insertion sort in Java Code
i: outer loop and j: the inner loop
Now we are going to the outer loop which we could use the variable i if we want to try this up**. **We could use i for this outer loop and the number of elements in the list which are 0 to 5 (0, 1, 2, 3, 4, and 5), we can use the variable key for our values, and j for our inner loop where compare to elements less than i moving from the left.
** 0 1 2 3 4 5**| 1 | 3 | 5 | 8 | 9 | 6 |
We are going to do an insertion sort using an array in Java. Here below is the code:
Example 1
public int[] insertionSort (int[] list) {
int i, j, key, temp;
for (i = 1; i < list.lenght; i++) {
key = list[i];
j = i - 1;
while (j >= 0 && key < list[j]) {
temp = list[j];
list[j] = list[j + 1];
list[j + 1] = temp;
j--;
}
}
return list;
}Let us study the code:
- Line 1: we are going to return an integer array, and insert an integer array, and we will assign it to the variable name called list.
- Line 2: Here we use some integer variables which is the outer loop, j is the inner loop, and then we have a ‘key’ value, and the ‘temp’ value to do the swap with.
- Line 3: we are going to use a ‘for loop’, and i = 1, we have started with 1 because the very first element 0 is already sorted, and the length of the list.
| 5 | 8 | 1 | 3 | 9 | 6 |
- i = 1 to 5 (It is from 1 to the end of the list which is 5).
- key = list[i] (The key is going to be initialized to the list of i which is starting from 1 to 5).
- j = i – 1 to 0 (j is the inner loop which has to count down form i – 1 to 0). If the first element of i is 1, that means j will 0 (j = 1 -1 which is equal to 0).
- Line 4: The value key is initialized to the list of ‘i’s.
- Line 5: The inner loop j which is equal to 1 minus 1.
- Line 6: The while loop: we want the while loop to iterate to the list i. So as long as j is greater and equal to 0, or key is less than the list j, we continue swapping.
public int[] insertionSort (int[] list) {
int i, j, key, temp;
for (i = 1; i < list.lenght; i++) {
key = list[i];
j = i - 1;
while (j >= 0 && key < list[j]) {
// swap
// swap
j--; // Here we are decrementing j (from left to the right)
}
}
return list;}Line 7 to Line 9: **Here are our swapping codes.
Example 2
A Java program to sort an array using Insertion sort algorithm
)
Code Output:
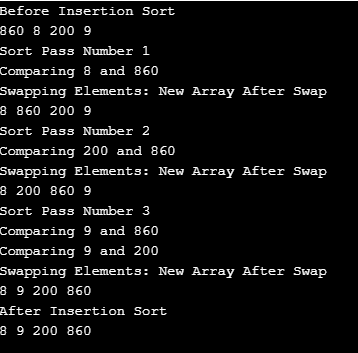
Example 3
We also provide Insertion sort algorithm in Java using ArrayLists below:
public ArrayList<Integer> insertionSort ArrayList<Interger> list){
int i, j, key, temp;
for (i = 1; i < list.size(); i++){
key = get(i);
j = i - 1;
while (j >= 0 && key < list.get(j)) {
temp = list.get(j);
list.set(j, list.get(j + 1));
list.set(j + 1, temp);
j--;
}
}
return list;
}